[Coding024] Sort - 归并排序
归并排序
Get the knowledge flowing and circulating! :)
目录
标题:归并排序
归并排序(英语:Merge sort,或mergesort),是建立在归并操作上的一种有效的排序算法,效率为
。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用,且各层分治递归可以同时进行。
Fig. 使用合并排序为一列数字进行排序的过程 概述
采用分治法:
分割:递归地把当前序列平均分割成两半;
集成:在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。
归并操作
归并操作(merge),也叫归并算法,指的是将两个已经排序的序列合并成一个序列的操作。归并排序算法依赖归并操作。
递归法(Top-down)
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
设定两个指针,最初位置分别为两个已经排序序列的起始位置
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
重复步骤3直到某一指针到达序列尾
将另一序列剩下的所有元素直接复制到合并序列尾
迭代法(Bottom-up)
原理如下(假设序列共有
个元素):
将序列每相邻两个数字进行归并操作,形成
个序列,排序后每个序列包含两/一个元素 若此时序列数不是1个则将上述序列再次归并,形成
个序列,每个序列包含四/三个元素 重复步骤2,直到所有元素排序完毕,即序列数为1
——维基百科
归并排序动画演示
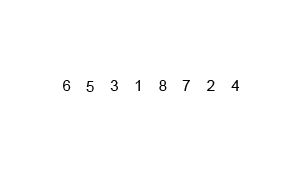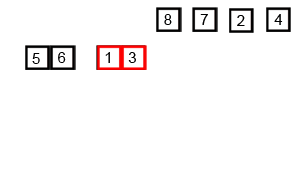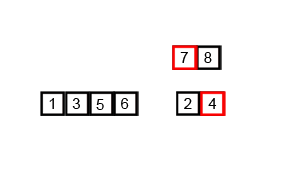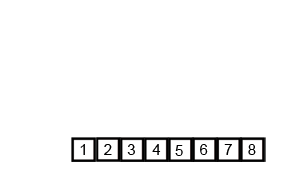
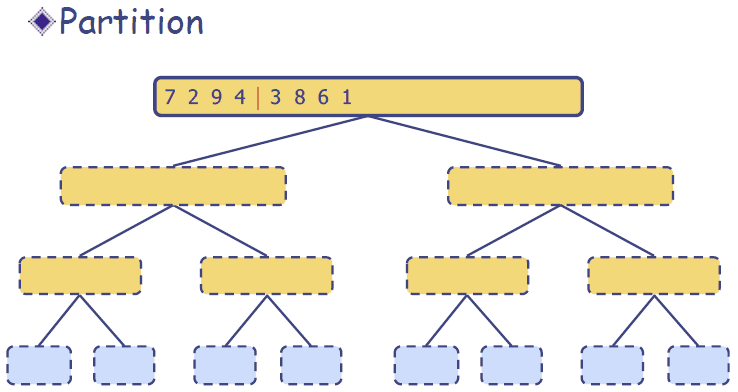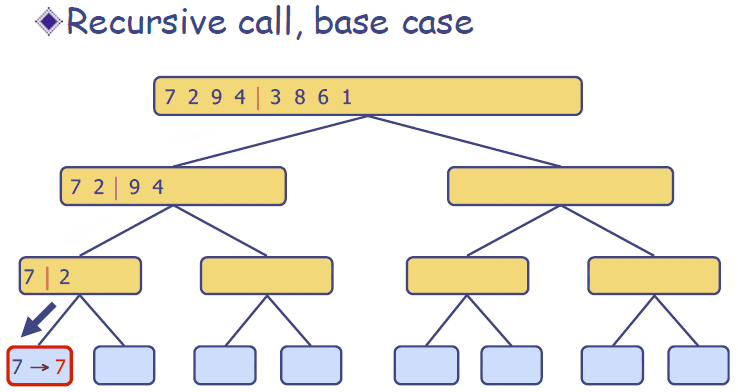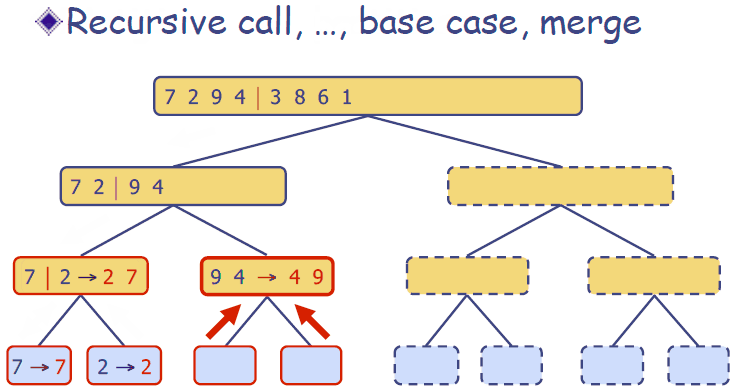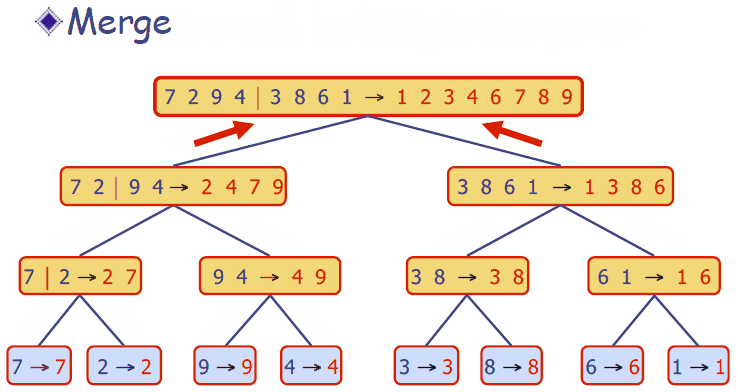

Java语言代码实现(版本1)
经典方法 - 两个函数
x
1import java.util.Scanner;2
3// 这是一个类,名叫Solution4public class Solution {5
6 /**7 * 归并排序 - 两个函数搞定8 */9 public static void main(String[] args) {10 // TODO Auto-generated method stub11 Scanner input = new Scanner(System.in);12
13 int n = input.nextInt();14 int[] arr = new int[n];15
16 for (int i = 0; i < n; i++) 17 {18 arr[i] = input.nextInt();19 }20
21 System.out.println("-------*--------");22
23 for (int e : arr)24 {25 System.out.print(e + " ");26 }27
28 System.out.println("\n-------*--------");29 Solution sol = new Solution();30
31 for (int len = 1; len < n; len = 2 * len) 32 {33 System.out.println("-----len: " + len);34 sol.MSort(arr, n, len);35 }36
37 for (int e : arr) 38 {39 System.out.print(e + " ");40 }41 return;42 }43
44 // Merge的功能:把一个范围,等分2份,排好45 public void Merge(int[] arr, int low, int mid, int high) 46 {47 // 左右2段48 // [low...mid], [mid + 1 ... high]49 int i = low;50 int j = mid + 1;51
52 // 合并为1段(新的)53 int k = 0;54 int[] newArr = new int[high - low + 1];55
56 while (i <= mid && j <= high) 57 {58 if (arr[i] > arr[j]) 59 {60 newArr[k] = arr[j];61 k++;62 j++;63 } 64 else 65 {66 newArr[k] = arr[i];67 k++;68 i++;69 }70 }71
72 while (i <= mid) 73 {74 newArr[k] = arr[i];75 k++;76 i++;77 }78
79 while (j <= high) 80 {81 newArr[k] = arr[j];82 k++;83 j++;84 }85
86 // 新的那段,再复制回原数组87 for (int s = low, t = 0; s <= high; s++, t++) 88 {89 arr[s] = newArr[t];90 }91 }92
93 // MSort的功能:按长度划分范围(长度为1时的划分、为2时的划分、...)94 public void MSort(int[] arr, int n, int length) 95 {96 int i;97 98 // length = 1时:99 // Merge(arr, 0, 0, 1)100 // Merge(arr, 2, 2, 3)101 // Merge(arr, 4, 4, 5)102 // Merge(arr, 6, 6, 7)103 // Merge(arr, 8, 8, 9)104 105 // length = 2时:106 // Merge(arr, 0, 1, 3)107 // Merge(arr, 4, 5, 7)108 109 // length = 4时:110 // Merge(arr, 0, 3, 7)111 for (i = 0; i + 2 * length - 1 < n; i = i + 2 * length) 112 {113 int low = i;114 int mid = i + length - 1;115 int high = i + 2 * length - 1;116 117 Merge(arr, low, mid, high);118
119 System.out.println("->" + low + "|" + mid + "|" + high);120 }121 // 上述的for循环退出后,i的值是(i+2*length),假如有9个数(n=9),i退出时为8。122
123 // ★★★124 // i + length - 1 = 8 < 9125 // 执行下面的程序126 if (i + length - 1 < n) 127 {128 int low = i;129 int mid = i + length - 1;130 int high = n - 1;131 Merge(arr, i, i + length - 1, n - 1); // Merge(8, 8, 8)132
133 System.out.println("==>" + low + "|" + mid + "|" + high);134 }135 }136
137}138/*139测试样例: 14051415 4 7 9 6142
1439 14465 70 75 80 85 60 55 50 45145
1461014710 20 30 40 50 60 70 80 90 100148
14920 15012 54 63 54 87 52 49 32 65 48 90 27 30 65 3 9 6 14 18 0151
1521015346 32 13 24 10 91 67 88 79 55154
1551015691 32 13 24 55 46 67 88 79 10157*/运行结果
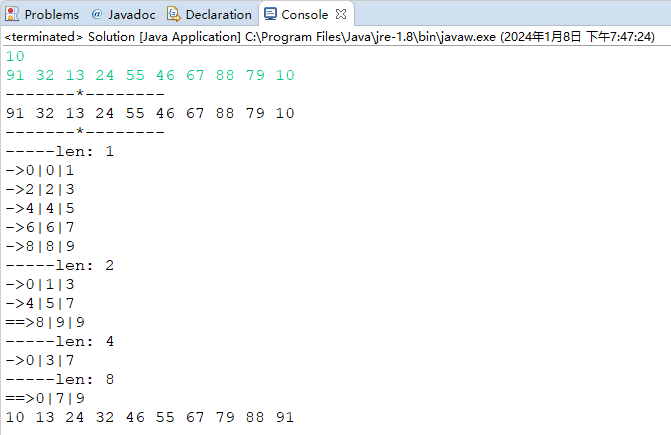
样例1:
x110291 32 13 24 55 46 67 88 79 10
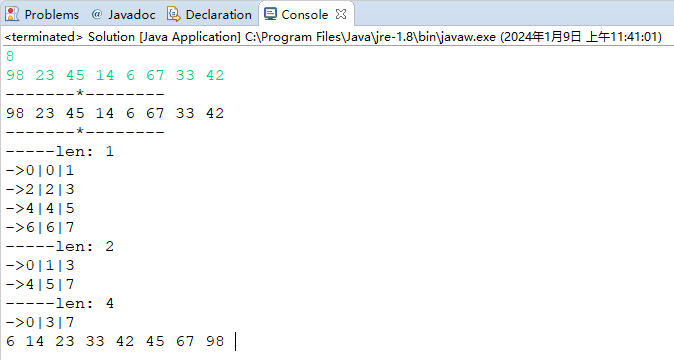
样例2:
xxxxxxxxxx218298 23 45 14 6 67 33 42
针对样例2的手绘图
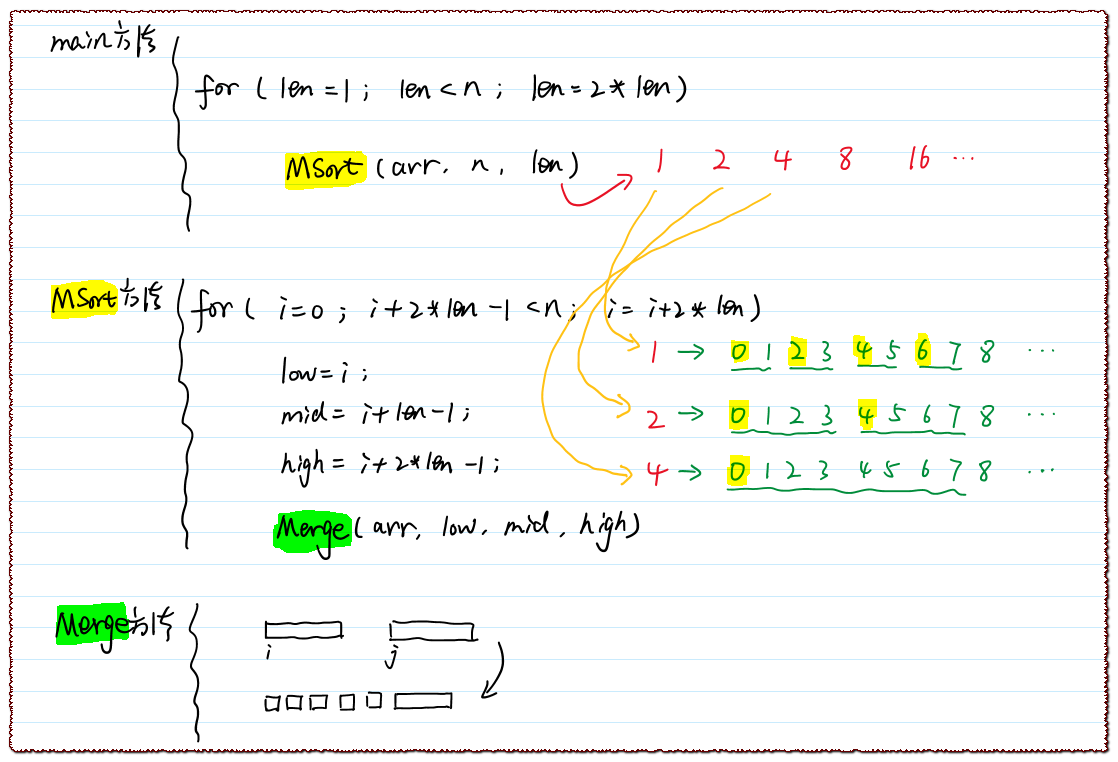
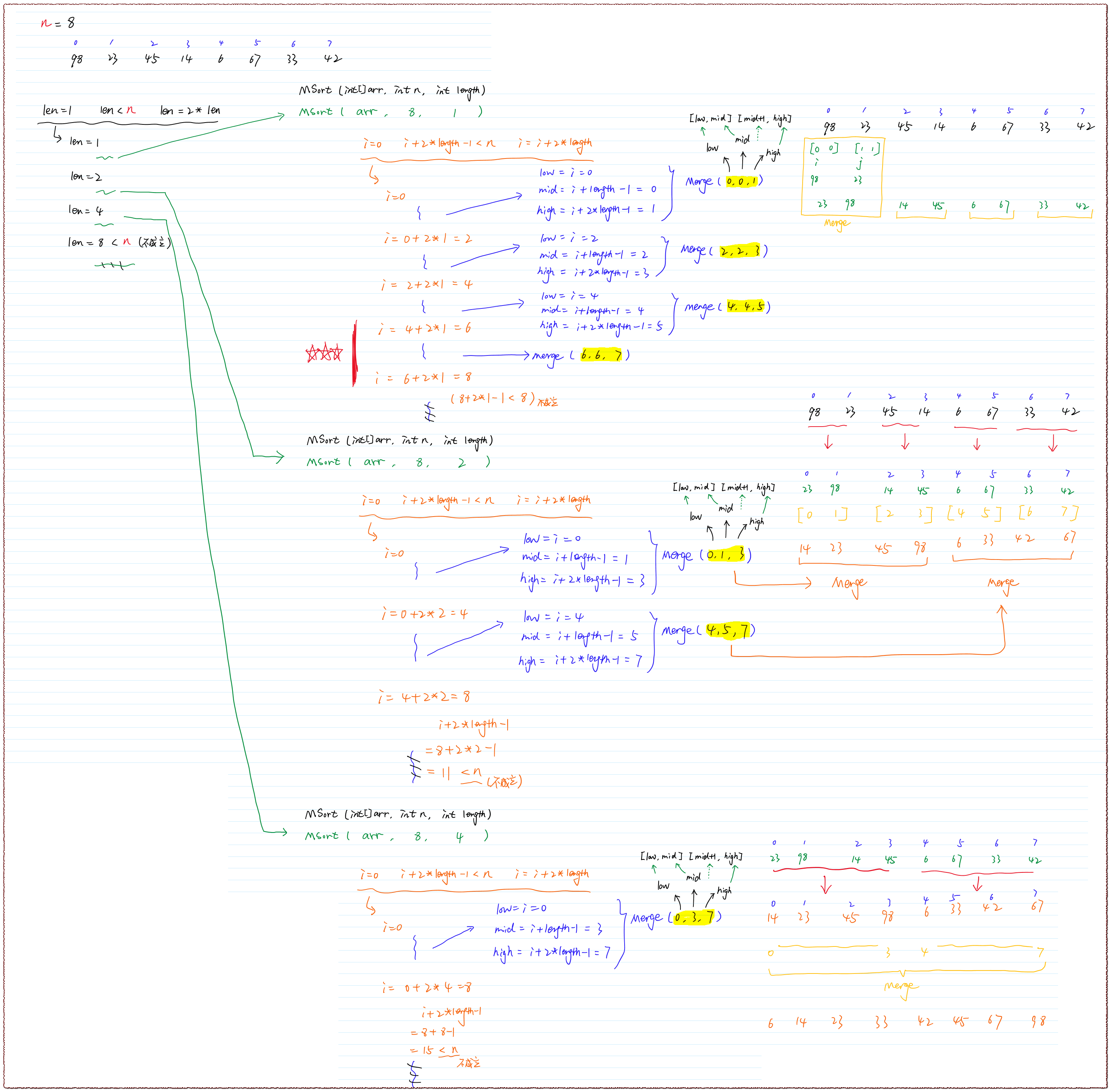
Java语言代码实现(版本2)
一个函数搞定(MergeSort,内置递归)
xxxxxxxxxx1101import java.util.Scanner;2
3// 这是一个类,名叫Solution4public class Solution {5
6 /**7 * 归并排序 - 一个函数搞定(MergeSort,内置递归)8 */9 public static void main(String[] args) 10 {11 // TODO Auto-generated method stub12 Scanner input = new Scanner(System.in);13
14 int n = input.nextInt();15 int[] arr = new int[n];16
17 for (int i = 0; i < n; i++) {18 arr[i] = input.nextInt();19 }20
21 System.out.println("---------------");22
23 for (int e : arr) {24 System.out.print(e + " ");25 }26
27 System.out.println("\n---------------");28 Solution sol = new Solution();29
30 int[] res = new int[n];31
32 res = sol.MergeSort(arr, 0, n - 1);33
34 for (int e : res) 35 {36 System.out.print(e + " ");37 }38 return;39 }40
41 public int[] MergeSort(int[] arr, int low, int high) 42 {43 if (low == high)44 return new int[] { arr[low] };45
46 int mid = low + (high - low) / 2;47
48 int[] arrLeft = MergeSort(arr, low, mid);49 int[] arrRight = MergeSort(arr, mid + 1, high);50 int[] newArr = new int[arrLeft.length + arrRight.length];51
52 int l = 0;53 int r = 0;54 int n = 0;55 56 while (l < arrLeft.length && r < arrRight.length) 57 {58 if (arrLeft[l] < arrRight[r]) 59 {60 newArr[n] = arrLeft[l];61 n++;62 l++;63 } 64 else 65 {66 newArr[n] = arrRight[r];67 n++;68 r++;69 }70 }71
72 while (l < arrLeft.length) 73 {74 newArr[n] = arrLeft[l];75 n++;76 l++;77 }78
79 while (r < arrRight.length) 80 {81 newArr[n] = arrRight[r];82 n++;83 r++;84 }85
86 return newArr;87 }88
89}90
91/*92测试样例: 935945 4 7 9 695
969 9765 70 75 80 85 60 55 50 4598
991010010 20 30 40 50 60 70 80 90 100101
10220 10312 54 63 54 87 52 49 32 65 48 90 27 30 65 3 9 6 14 18 0104
1051010646 32 13 24 10 91 67 88 79 55107
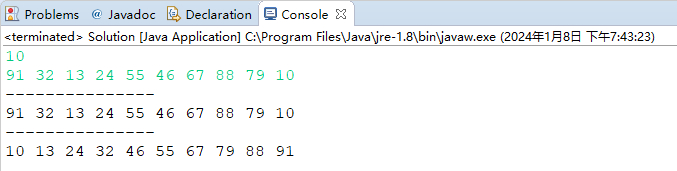
1081010991 32 13 24 55 46 67 88 79 10110*/运行结果
复杂度
| 平均时间复杂度 | |
|---|---|
| 最坏时间复杂度 | |
| 最优时间复杂度 | |
| 空间复杂度 | |
| 最佳解 | 有时是 |
复杂度分析
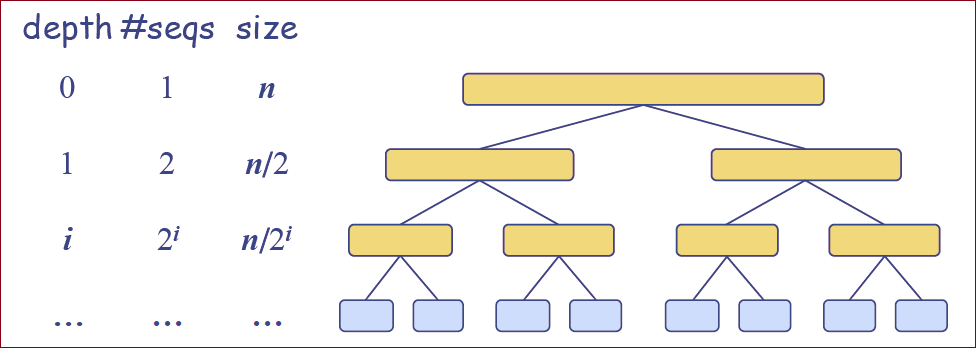
※ 归并排序树的高度
是
每一次调用的时候我们都把序列分为两部分;
※ 深度为
的那层的节点总数是
我们切分与合并了
个长度为 的序列; 我们进行了
次递归调用; 所以,归并排序的整体运行时间为
。
稳定性
归并排序是否稳定排序取决于比较条件中,左边的元素和右边的元素比较情况:
如果是左边元素 <= 右边元素
new = 左边元素(小于等于的时候,都是先取左边元素)【稳定】
else
new = 右边元素
如果是左边元素 < 右边元素
new = 左边元素(小于的时候,先取左边元素)
else
new = 右边元素(大于等于的时候,取右边元素)【不稳定】